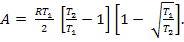(2019).9.5

Найдите работу А, совершаемую одним молем (υ=1) идеального газа в цикле (1⟼2⟼3⟼1), состоящем из двух участков линейной зависимости давления от объема и изохоры (см. рис.). Точки 1 и 2 лежат на одной прямой, проходящей через начало координат (на диаграмме PV). Температуры Т₁ и Т₂ в соответствующих точках 1 и 2 известны. Т₃ = Т₁.

• Решение

Решение

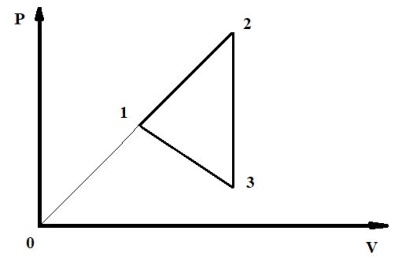
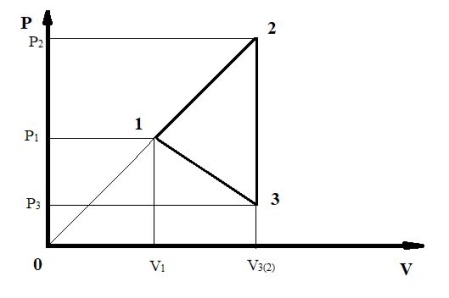
Даны два рисунка: исходный (левый) из условия задачи и подготовленный для решения задачи (правый), которым мы будем в дальнейшем пользоваться.

Работа, совершаемая газом на каждом участке цикла, численно равна площади трапеции, заключенной между графиком процесса, осью V, и двумя перпендикулярами, опущенными из начальной и конечной точек процесса на ось V. Работа, совершаемая газом, положительна, если газ в соответствующем процессе (1⟼2, например) расширялся. Работа, совершаемая газом, отрицательна, если газ в соответствующем процессе (3⟼1, например) сжимался. Два последних утверждения легко доказываются в общем виде. Работа, совершаемая газом за весь цикл, численно равна площади фигуры (в нашем случае это треугольник 1,2,3), ограниченной графиками процессов, составляющих цикл.

Работа А_1⟼2 , совершаемая газом на участке цикла (1⟼2) равна

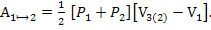 (1)

Работа А_3⟼1, совершаемая газом на участке цикла (3⟼1) равна

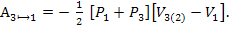
(2)

При вычислении работ А_1⟼2 и А_3⟼1 была применена хорошо известная формула для вычисления площади трапеции: площадь трапеции равна произведению полусуммы оснований трапеции на высоту трапеции.

Работа А_2⟼3, совершаемая газом на участке цикла (2⟼3) равна нулю (изохорический процесс).

Таким образом, работа, совершаемая газом за весь цикл, равна

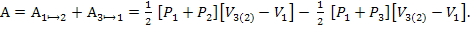(3)

Раскрывая в последнем выражении скобки, и, применяя (где это уже можно) уравнение Клапейрона-Менделеева (для данного моля газа)

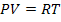(4)

преобразуем выражение для работы, совершаемой газом за весь цикл







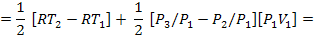
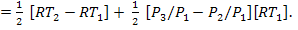(5)

Из рисунка можно получить дополнительные соотношения между термодинамическими величинами в точках цикла 1,2,3. Из двух подобных прямоугольных треугольников, вершины которых «обозначены точками» (0,2,V₃₍₂₎) и (0,1,V₁) можно получить

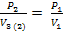 (6)

Так, как точки 1 и 3 лежат (по условию) на одной изотерме (она из-за ненадобности не нарисована на рисунке), можно записать

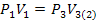 (7)

Из выражений (6) и (7) следует




или, что то же самое,

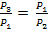 (8)

Из изохоры (2⟼3) получаем

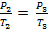(9)

или, что то же самое,

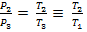 (10)

Выражение (10) с учетом выражения (8) можно преобразовать




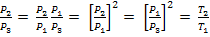
Отсюда получаем

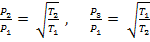 (11)

После подстановки выражений (11) в выражение (5) и, после простых преобразований, получаем окончательное выражение для работы, совершаемой газом за весь цикл

Итого: 

• Ответ

Ответ

Смотри решение