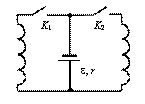
Решение
После замыкания ключа K2 напряжения на концах обеих катушек в любой момент времени будут равны друг другу. Так как активные сопротивления катушек равны нулю, это условие записывается в виде равенства ЭДС самоиндукции:
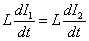 ,
,где L – индуктивности катушек, I1 и I2 – силы токов в катушках.
Отсюда:
I1(t) – I2(t) = const, (1)
то есть, при замкнутых ключах разность абсолютных значений сил токов в катушках остается неизменной в любой момент времени.
Силу тока через первую катушку в момент замыкания ключа K2 обозначим через I0:
I1(t=0) = I0,
(I0 является искомой величиной задачи).
В этот же момент времени сила тока через вторую катушку равна нулю:
I2(t=0) = 0.
Согласно (1) получим:
I1(t) – I2(t) = I1(t=0) – I2(t=0) = I0 = const. (2)
В установившемся режиме через катушки будут течь постоянные токи, которые обозначим через Iуст.1 и Iуст.2. При этом разность потенциалов на концах катушек равна нулю, и, следовательно, сила тока через источник Iист равна:
Iист = e/r.
По правилу Кирхгофа для сил токов имеем:
Iуст.1 + Iуст.2 = Iист = e/r. (3)
Кроме того, по условию задачи:
Iуст.1 / Iуст.2 = 2. (4)
Из уравнений (3) и (4) находим:
Iуст.1 = 2e/(3r), Iуст.2 = e/r.
В соответствии с (2) находим искомую величину:
I0 = Iуст.1 – Iуст.2 = e/(3r).