(2022).11.3
В теплоизолированный сосуд, закрытый теплоизолированным поршнем, помещена смесь водяного пара и воды при температуре T кельвинов (масса воды много меньше массы пара). Поршень сместили, в результате объем системы уменьшился, температура пара возросла на DT, причем DT<<T, а часть воды испарилась. Найти отношение массы испарившейся воды к массе пара в исходном состоянии. Удельная теплота испарения при температуре T равна l Дж/кг, пар можно считать идеальным газом с молярной теплоемкостью при постоянном объеме равной CV Дж/(моль×К). Теплоемкостью воды пренебречь. Также известно, что малые относительные изменения температуры DT/T связаны с относительными изменениями давления насыщенного пара Dp/p соотношением Dp/p = kDT/T, где k – положительная константа. Молярная масса воды m кг/моль.
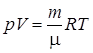 . (1)
. (1) 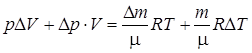 . (2)
. (2) 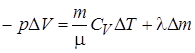 . (3)
. (3) 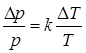 . (4)
. (4)