Архив задач

(2021).11.2

В горизонтально расположенном цилиндрическом сосуде длины L находятся n подвижных, физически бесконечно тонких, теплонепроницаемых поршней, делящих сосуд на n+1 отсек. Первоначально объемы всех отсеков одинаковы, температура газов во всех отсеках равна Т0. Затем газ в самом левом отсеке нагревают до температуры Т (Т>Т0). При этом в других отсеках поддерживают прежнюю температуру Т0. На какое расстояние ΔL сместится самый правый поршень? 


  • Решение

    • Решение

    Начальное состояние газа во всем цилиндрическом сосуде описывается уравнением состояния:

    image028.png

    Число молей газа в каждом отсеке ν1 до и после нагревания самого левого отсека одинаково и равно:

    image029.png

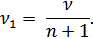
    Тогда число молей в самом левом отсеке νл и во всех остальных (правых) отсеках νправ. соответственно равны:

    image030.png

    image037.png

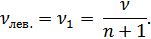
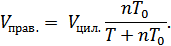
    Запишем уравнение состояния газов в самом левом и во всех правых отсеках соответственно после нагревания самого левого отсека:

    image032.png

    image033.png

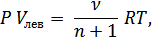
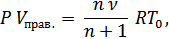
    Поделив друг на друга последние выражения, получим отношение объемов, которые занимают нагретый газ в самом левом отсеке и газ во всех остальных (правых отсеках):

    image034.png

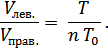
    При этом должно выполняться равенство (условие постоянства объема всего цилиндрического сосуда длины L):

    image035.png

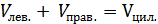
    Из последних двух выражений находим:

    image036.png

    image037.png

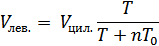
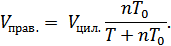
    Из последнего выражения найдем объем, приходящийся на каждый правый отсек:

    image038.png

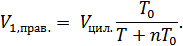
    До нагревания самого левого отсека, на каждый отсек приходился объем

    image039.png

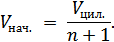
    Тогда, чтобы найти расстояние ΔL (на которое сместится самый правый поршень) после нагревания самого левого отсека, надо из последнего выражения вычесть предпоследнее выражение, и результат поделить на площадь сечения цилиндрического сосуда S

    image040.png

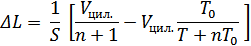
    Проведя простые преобразования (с учетом естественного соотношения 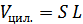image041.png ), получим ответ. 

  • Ответ

    • Ответ

    image042.png