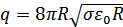(2021).11.5

Известно, что капля жидкости в невесомости принимает сферическую форму, обусловленную собственным поверхностным натяжением, величина которого определяется коэффициентом поверхностного натяжения σ. В этом случае на единицу поверхности капли радиуса R действует сила PL=2σ/R (лапласовское давление), направленная внутрь поверхности и перпендикулярная ей. Пусть теперь на каплю поместили заряд q, равномерно распределенный по ее поверхности. Найти величину q, при которой капля может потерять сферическую форму. Величины σ и R известны. Используя полученное выражение для q, рассчитать q при σ=0,073 н/м и R=1 см. 

• Решение

Решение

Если на поверхность капли поместить равномерно распределенный заряд, то за счет того, что элементарные одноименные заряды отталкиваются и будут стремиться удалиться друг от друга, т.е. растянуть каплю, будет возникать сила отрицательного давления Pэ на ее поверхность. Эта сила направлена наружу по отношению к поверхности капли и перпендикулярна ей.

Найдем силу давления Pэ из условия, что работа Aэ этой силы равна изменению энергии ΔW при расширении заряженной сферы, то есть изменении ее радиуса на малую величину Δr.



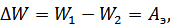
где W₁ – энергия электрического поля при радиусе заряженной сферы равном r, а W₂ – энергия электрического поля при радиусе заряженной сферы равном r+Δr, где Δr<< r. При выполнении условия малости Δr изменением плотности заряда при расширении сферы можно пренебречь.

Найдем работу из условия, что энергия электрического поля сферы ΔW, заключенная в тонком слое Δr, равна



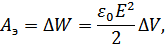
где - 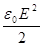 плотность энергии электростатического поля у поверхности сферы (внутри сферы поле равно нулю), - ΔV изменение объема при ее расширении.

С другой стороны работа силы давления Pэ равна:



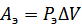
Приравнивая выражения, получим:



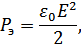
где 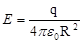 , тогда



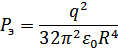
Сферическая форма капли может нарушиться, когда лапласовское давление будет скомпенсировано отрицательным давлением из-за электрического заряда:

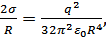 отсюда    

• Ответ

Ответ

q=20 нКл