Решение
Вблизи верхней точки траектории скорость монеты мала, и сопротивлением воздуха можно пренебречь. Тогда на монету действуют: сила тяжести Fт, выталкивающая сила (сила Архимеда) FA и сила со стороны магнитного поля Fм.
Сила тяжести:
,
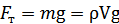где m – масса монеты, V – ее объем.
Сила Архимеда:
FA= ρвVg.
Следовательно,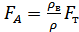 
.
Теперь найдем силу, действующую на монету со стороны магнитного поля. Пусть монета имеет площадь плоской поверхности S и толщину l и движется в магнитном поле так, что ее плоскость параллельна силовым линиям. На электроны внутри монеты будет действовать сила Лоренца, направленная перпендикулярно плоскости монеты. Такая же, но направленная в противоположную сторону, сила будет действовать на положительные ионы металла. Магнитное поле стремится растащить положительные и отрицательные заряды в противоположные стороны. Но смещение зарядов вызовет появление электрического поля, удерживающего заряды. Из условия равенства этих сил находим, что напряженность электрического поля E=vB. Таким образом, между двумя сторонами монеты возникнет разность потенциалов U= vBl.
Такое же поле создает плоский конденсатор с расстоянием между обкладками l и площадью обкладки S. Заряд конденсатора:
.
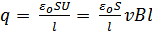Если пластинка будет двигаться с ускорением a, то заряд будет изменяться:
.
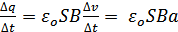Это равносильно появлению тока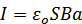 
.
На проводник с током будет действовать сила Ампера:
.
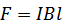Следовательно, на монету, движущуюся с ускорением, будет действовать сила:
.
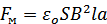По второму закону Ньютона для падающей монеты:
.
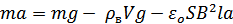Или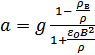 
.
Таким образом, магнитное поле уменьшает ускорение. Магнитное поле с индукцией в 30 Тл – это очень сильное постоянное магнитное поле, получаемое в лабораториях с помощью мощных электромагнитов. Однако, подставляя значения магнитной индукции и плотности в знаменатель формулы для ускорения, получаем, что величина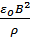 
пренебрежимо мала по сравнению с единицей. Таким образом
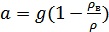= 9,815 м/с2.
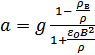