(2020).9.4

На горизонтальной поверхности стола покоится доска массы M. На горизонтальной верхней поверхности этой доски покоится другая доска массы m. Коэффициент трения скольжения между досками равен μ. Коэффициент трения скольжения между нижней доской и столом равен нулю. К верхней доске приложили горизонтальную силу F (см. рис). Найти ускорения a_н и a_в нижней и верхней досок и силу трения F_тр., возникающую между досками. 

• Решение

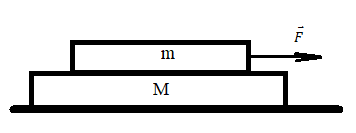
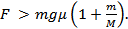Решение

Проанализируем все возможные случаи.

1. Приложенная к верхней доске сила равна нулю (F=0). Тогда:

.

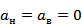Сила трения (сила трения покоя) тоже равна нулю

.

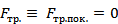2. Приложенная к верхней доске сила не равна нулю (F≠0) и тела движутся как единое целое.

В этом случае ускорения тел легко вычисляются и равны:



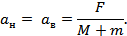
Поскольку нижняя доска движется с только что найденным ускорением a_н благодаря лишь силе трения (силе трения покоя, т.к. доски не движутся друг относительно друга), находим:

.

Однако, величина силы трения покоя всегда ограничена сверху величиной силы трения скольжения:



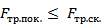
Подставляем в последнее неравенство выражения для соответствующих сил, найдем предельную силу F, при которой доски еще могут двигаться как единое целое:



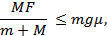
или

 .

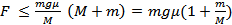Если внешняя сила F будет удовлетворять неравенству



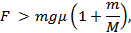
доски будут двигаться не как единое целое (одна относительно другой).

3. Приложенная к верхней доске сила не равна нулю (F≠0) но тела движутся не как единое целое. Напишем уравнения движения для каждой из досок:





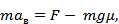
где 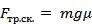. – сила трения скольжения.

Запишем решения этих уравнений:





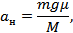
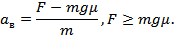
Неравенство 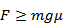 – это требование того, чтобы величина  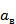была неотрицательна.

Не трудно доказать, что неравенство 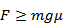 заведомо выполнимо, т.к. выполняется неравенство   

• Ответ

Ответ

1.  ,  , если F=0. Доски покоятся друг относительно друга и относительно стола.

2. ‚ , если  Доски покоятся друг относительно друга, но как единое целое движутся относительно стола.

3.   если   Доски движутся и относительно друг друга , и относительно стола.