Решение
Нарисуем рисунок, соответствующий условию задачи. Этот рисунок соответствует нашей работе в так называемой лабораторной инерциальной системе отсчета (ЛИСО), связанной с землей.
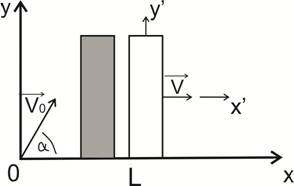
Шарик в момент броска находится в начале координат. Левая сторона стенки в момент броска шарика находится в точке, отстоящей от начала координат на расстоянии 
(она не дана по условию задачи). Координаты шарика (в ЛИСО) изменяются со временем по закону:
Координата левой стороны стенки 
изменяется со временем по закону:
Здесь – начальное расстояние от начала координат до стенки: 
.
В момент 
соударения шарика со стенкой 
, или 
Отсюда получаем время соударения:
(1)
Из положительности получаем 
Это физическое условие того, что брошенный шарик «догонит» удаляющуюся от него стенку.
Кроме того, можно записать искомое расстояние 
(вдоль горизонта) от точки бросания шарика до точки его столкновения со стенкой:
(2)
Запишем проекции скоростей шарика на оси координат:
Для простоты и наглядности дальнейшего решения задачи перейдем в движущуюся инерциальную систему отсчета (ДИСО), связанную со стенкой. В этой ДИСО скорость стенки равна нулю, а скорость шарика 
равна
где 
скорости шарика и стенки в ЛИСО.
В проекции на ось х:
Акт упругого соударения шарика с очень тяжелой (по условию задачи) стенкой в ДИСО описывается очень просто:
.
В левой части этого равенства записана проекция скорости шарика (в ДИСО) в момент времени 
, следующий после столкновения шарика с неподвижной стенкой.
В правой части этого равенства записана проекция скорости шарика (в ДИСО) в момент времени 
, предшествующий столкновению шарика с неподвижной стенкой.
Само время упругого столкновения шарика со стенкой равно нулю.
Путем простых преобразований найдем проекцию скорости шарика на ось х 
(в ЛИСО) после соударения шарика со стенкой.
Поскольку шарик после соударения со стенкой летит в сторону, противоположную направлению оси (чтобы вернуться согласно условию задачи в точку бросания – начало координат), потребуем, чтобы выполнялось условие
Далее работаем только в ЛИСО.
Пусть 
– время полета шарика от момента столкновения со стенкой до возвращения в точку бросания.
Опишем движение шарика от момента столкновения со стенкой до возвращения в точку бросания.
В момент возвращения шарика в начало координат:
(3)
Обратим внимание на еще одно простое соотношение между неизвестными величинами задачи, являющееся следствием того, что шарик после упругого соударения со стенкой возвращается в точку бросания:
(4)
Из последнего равенства следует:
(5)
Рассмотрим теперь движение шарика вдоль вертикальной оси координат – оси . Это -движение тела, брошенного вертикально вверх в поле сил тяжести. На это движение никак не влияет соударение шарика со стенкой. Время полета шарика до возвращения в начало координат хорошо известно:
(6)
Решая совместно (3),(4),(5),(6), отвечаем на вопросы задачи:
где 
Заменив во всех ответах к задаче 
на
, мы получим решение аналогичной задачи, в которой стенка движется на встречу брошенному шарику (сделайте это самостоятельно).
под углом 
к горизонту, упруго ударяется о вертикальную (очень тяжелую) стенку, движущуюся с постоянной скоростью 
и 
лежат в одной плоскости. Известно, что после соударения со стенкой, шарик возвращается в ту точку, откуда его бросили. Через какое время